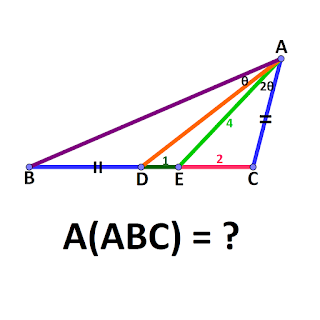This question is uploaded on Instagram on page "@gercekboss" on 12th of June 2020. I provided Instagram link of this question. Click here to go to that question.
Take a look at figure given below. Give it a try and when you are ready then watch the solution.
In triangle ABC, CE = 2, ED = 1, AE = 4, ∠CAE = 2θ, ∠BAD = θ, AC = BD. Find Area of triangle ABC. One of the Hard puzzle on Instagram.
First rotate this figure such that it would be easy to understand and constructions that I will make will be easy for all.
Note: I don't needed that angles while solving this puzzle but may be by any other method that angles maybe useful.
Draw AF || BC
Draw DG || AC
Draw BF || AC
Step 2:
DC = AG = 3
AC = BD = DG = GF = BF = x
□ACBF is a parallelogram (AC = BF; BC = AF)
Step 3: Similarity in △BDH and △AGH
Angles at H for both are same (Vertically opposite angles)
Angles at G and D are same (Alternate angles)
Angles at A and B are same (Alternate angles)
⇒ △BDH ~ △AGH\[\Rightarrow\frac{GH}{DH}=\frac{AG}{BD}\]
\[\Rightarrow\frac{GH}{DH}=\frac{3}{x}\]
and also
\[\frac{GH}{DH}=\frac{AH}{BH}\]
Step 4: Similarity in □BFGH and □ACDH
Angles at H for both are same (Vertically opposite angles)
Angles at G and D are same (Alternate angles)
Angles at A and B are same (Alternate angles)
Angles at F and C are same (Alternate angles)
⇒ □BFGH ~ □ACDH
But one side is same (BF = AC = x)
And GH:DH = AH:BH
⇒ □BFGH ≅ □ACDH
⇒ GF = DC
⇒ x = 3
Step 5: Calculate length of all sides
AC = x = 3
BC = x+3 = 6
Now apply cosine rule on △AEC and △ABC at angle α
\[\Rightarrow\frac{2^2+3^2-4^2}{2\times2\times3}=\frac{3^2+6^2-AB^2}{2\times3\times6}\]
\[\Rightarrow -3=\frac{45-AB^2}{3}\]
\[\Rightarrow -9=45-AB^2\]
\[\Rightarrow AB^2=54\]
\[\Rightarrow AB=\sqrt{54}\]
\[\Rightarrow AB=3\sqrt{6}\]
Step 6:
Now apply Herons formula to calculate Area of Triangle ABC
\[s=\frac{9+3\sqrt{6}}{2}\]
Now calculate area
\[A=\sqrt{\left(\frac{9+3\sqrt{6}}{2}\right)\left(\frac{9-3\sqrt{6}}{2}\right)\left(\frac{3\sqrt{6}+3}{2}\right)\left(\frac{3\sqrt{6}-3}{2}\right)}\]
\[A=\sqrt{\left(\frac{81-54}{4}\right)\left(\frac{54-9}{4}\right)}\]
\[A=\sqrt{\frac{27\times45}{16}}\]
\[A=\frac{9\sqrt{15}}{4}\]
In this method we got area = 9√15 / 4