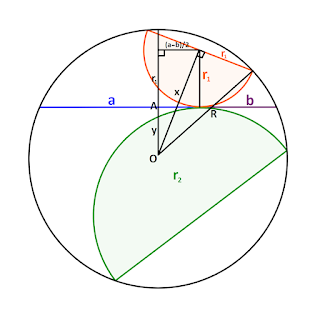
This question was uploaded on 25/11/21 on social media accounts.
Solution:
Line with length 'x' is part of two right angled triangles:
\[x^2 = (y+r_1^2)+\left(\frac{a-b}2\right)^2 = R^2-r_1^2\]
Intersecting chord theorem on point A:
\[(R-y)(R+y) = \left(\frac{a+b}2\right)^2\]
From the above two equations:
\[2r_1^2+2yr_1+ab=0\]
\[\Rightarrow 2r_1 = -y + \sqrt{y^2+2ab}\]
If we replace y with -y then we will get the value for r2:
\[\Rightarrow 2r_2 = y + \sqrt{y^2+2ab}\]
Now,
\[4.r_1.r_2 = \left(-y + \sqrt{y^2+2ab}\right)\left(y + \sqrt{y^2+2ab}\right)\]
\[\Rightarrow 4.r_1.r_2 = y^2 +2ab - y^2\]
\[\Rightarrow 4.r_1.r_2 = 2ab\]
\[\Rightarrow \frac{a.b}{r_1.r_2} = 2\]