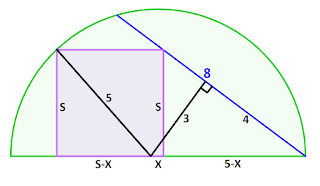
This question was uploaded on 13/12/21 on social media accounts.
Solution 1:
Right side triangles with sides (3, 4, 5) and (S, 5-X, Blue Line):
\[\frac{S}{5-X} = \frac34\]
Triangle inside the square with sides (S, S-X, 5):
\[S^2+(S-X)^2 = 5^2\]
From both equations:
\[S = \frac{105}{29}\]
Solution 2:
\[a(10-a) = S^2\]
Triangles with sides (6, 8, 10) and (S, 10-(a+S), Blue Line):
\[\frac{S}{10-(a+S)} = \frac68\]
From both equations:
\[S = \frac{105}{29}\]