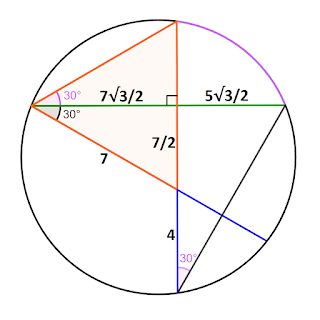
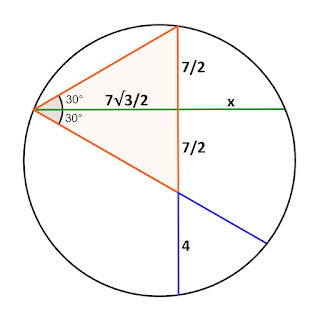
This question was uploaded on 09/01/22 on social media accounts.
Solution 1:
By Ptolemy's theorem:
\[\color{red} {(7)(x)+(11)(x)=(L)(x\sqrt3)}\]
\[\color{red} {\Rightarrow L=6\sqrt3}\]
Solution 2:
\[\color{green} {Green=\frac72\sqrt3+\frac52\sqrt3}\]
\[\color{green} {\Rightarrow Green=6\sqrt3}\]