Dare2Solve | Triangle and rectangle inside a parallelogram separated by a diagonal

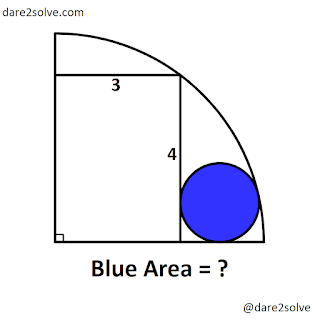
This question was uploaded on 24/11/21 on social media accounts.

Solution:

Here FM and CD are parallel and also EM and BC are parallel.

Areas of ABC and ACD are same due to diagonal and parallelogram.

FM = 2CD also EM = 2BC

By the above information:

Red area is one-fourth of are of ACD and Blue area is half of area of ABC.

That means Blue Area is twice of Red Area.

So Blue Area = (2)(5) = 10

Dare2solve | Rectangle and circle in a quarter circle

This question was uploaded on 21/11/21 on social media accounts.

Solution:

The radius of the quarter circle is 5 by the hypotenuse theorem.

Let the radius of the small circle be 'r'.

\[(5-r)^2=r^2+(3+r)^2\]

\[\Rightarrow r = 4\sqrt5-8\]

Area:

\[A= \pi r^2 = (144-16\sqrt5)\pi\]

or

\[A= 16(9-4\sqrt5)\pi\]

Dare2solve | Area of rectangle made by two 30-60-90 triangles

This question was uploaded on 03/11/21 on social media accounts.

Solution:

Length of rectangle = x + y

\[\Rightarrow 2a\sqrt3=\sqrt{1-a^2}+\sqrt{4-a^2}\]

\[\Rightarrow a^2=\frac{5+\sqrt{13}}{16}\]

Blue Area:

\[Area = (2a)(2a\sqrt3)=4a^2\sqrt3\]

\[\Rightarrow Area = \frac{\sqrt3}4\cdot(5+\sqrt{13})\]

Dare2solve | Ratio of areas of triangle and rectangle

This question was uploaded on 23/10/21 on social media accounts.

A triangle is inscribed in a rectangle with the base on one side of the rectangle. Another rectangle passes through the base of the triangle and two vertex touch sides of the rectangle. Find the ratio of areas of triangle and rectangle.

Solution:

By area of triangle:

Orange = Green

Also,

Blue = Orangle

Now:

Area of triangle : Area of Rectangle = 1 : 2

Puzzle related to Geometry, Triangle, Rectangle, Area, Ratio.

Dare2solve | Semicircle and Rectangle - Area of rectangle

This question was uploaded on 22/10/21 on social media accounts.

A rectangle and a semicircle are drawn such that one vertex is the same and one side of the square is passing through the top of the semicircle. The length of the chord from the common vertex to the common point is given. Find the area of the rectangle.

Solution 1:

By two right-angled triangles in the figure:

\[x^2=r^2-a^2=2^2-(r+a)^2\]

\[\Rightarrow r^2-a^2=4-r^2-a^2-2ar\]

\[\Rightarrow r(a+r)=2\]

\[Area=r(a+r)=2\]

Solution 2:

\[r=\frac{a+b}2\]

By right-angled triangle:

\[x^2=2^2-b^2\]

By intersecting chord theorem:

\[x^2=ab\]

\[\Rightarrow 4-b^2=ab\]

\[\Rightarrow (a+b)b=4\]

\[Area = rb = \left(\frac{a+b}2\right)b=2\]

Puzzle related to Geometry, Circle, Rectangle, Area.

Dare2solve | Square and rectangle in a circle - chord is colinear with diagonal of the square

This question was uploaded on 29/09/21 on social media accounts.

A square and a rectangle combined to form another rectangle are inscribed in a circle. A chord of length 5 units is made by extending the diagonal of the square.

Solution 1:

Chord theorem:

\[(a\sqrt2)(5-a\sqrt2)=(a)(b)\]

\[\Rightarrow 2a+b=5\sqrt2\]

Perimeter (ABCD):

\[P = 4a+2b\]

\[\Rightarrow P = 2(5\sqrt2) = 10\sqrt2\]

Solution 2:

Triangle 1 and Triangle 2 are similar:

\[\Rightarrow \frac{5-a\sqrt2}{b}=\frac{a}{a\sqrt2}\]

\[\Rightarrow 2a+b=5\sqrt2\]

Perimeter (ABCD):

\[P = 4a+2b\]

\[\Rightarrow P = 2(5\sqrt2) = 10\sqrt2\]

Solution 3:

The beautiful solution from Twitter:

Puzzle related to Geometry, Square, Rectangle, Length.