2021-12-07
2021-11-08
This question was uploaded on 07/11/21 on social media accounts.
Solution:
We know that:
\[a^2+b^2+c^2+d^2=4r^2\]
Click here to read the proof of this identity.
\[Orange = \pi r^2\]
\[Green = a^2+b^2+c^2+d^2=4r^2\]
\[\frac{Orange}{Green}=\frac{\pi r^2}{4r^2}=\frac\pi4\]
2021-11-01
This question was uploaded on 31/10/21 on social media accounts.
Two lines in a square from a vertex inclined with equal angle. Find the area under both lines and sides of the square.
Solution:
Triangle with two red sides is an equilateral triangle.
One triangle is 6-8-10 triangle.
The side of the square is 8.
\[Area=\frac{(4)(8)}2+\frac{(2)(8)}2=24\]
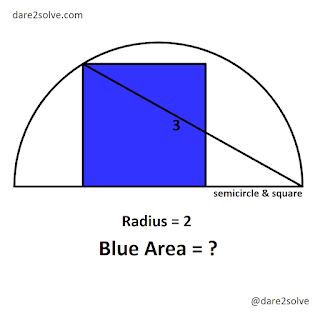
2021-10-30
This question was uploaded on 29/10/21 on social media accounts.
Square in a semicircle such that one line can pass through one end of diameter and two opposite edges of the square. One edge of the square is on the origin and one on the semicircle.
Solution:
Purple triangle is an equilateral triangle.
By inscribed angle theorem:
\[x=\frac{60+45}2=\frac{105}2=72.5\]
Puzzle related to Geometry, Circle, Square, Angle.
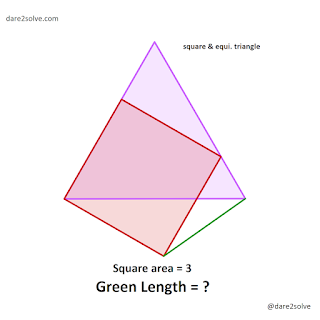
2021-10-27
This question was uploaded on 26/10/21 on social media accounts.
Square and an equilateral triangle such that one side of the square is on one side of the triangle and also one vertex for both figures is the same.
Solution:
Green Length (By cosine rule):
\[\cos30 = \frac{(\sqrt3)^2+(1+\sqrt3)^2-x^2}{2(\sqrt3)(1+\sqrt3)}\]
\[\Rightarrow x^2 = 4-\sqrt3\]
\[\Rightarrow x = \sqrt{4-\sqrt3}\]
Puzzle related to Geometry, Length, Square, Triangle.
2021-10-26
This question was uploaded on 25/10/21 on social media accounts.
Find the ratio of the area between the equilateral triangle and the square to the complete area of the figure. Square is placed on the base of the triangle as shown in the figure.
Solution 1:
Now you can see 1 small equilateral triangle (1), one rectangle (3), and three 30-60-90 triangles (2, 4, 5).
Areas:
\[A_1=\frac{\sqrt3}4(\sqrt3-1)^2=\frac{\sqrt3}2(2-\sqrt3)\]
\[A_2=A_4=A_5=\frac{1\times\sqrt3}2=\frac{\sqrt3}2\]
\[A_3=\sqrt3(\sqrt3-1)\]
Blue fraction:
\[Fraction=\frac{A_3+A_4}{A_1+A_2+A_3+A_4+A_5}\]
\[\Rightarrow Fraction=\frac{2\sqrt3-1}{3+\sqrt3}=\frac{7\sqrt3-9}6\]
Puzzle related to Geometry, Square, Triangle, Ratio.
2021-10-21
This question was uploaded on 20/10/21 on social media accounts.
Two squares with one same vertex and one side is passing through the vertex of another square.
Solution:
Angle 45 is the same due to the angle inscribed in the same arc.
\[\alpha+45=90\]
\[\Rightarrow\alpha=45\]
Puzzle related to geometry, square, angle.