This question was uploaded on 09/08/21 on social media accounts.
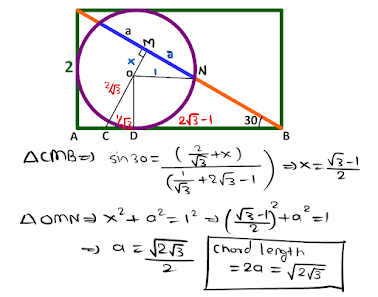
A rectangle is given with small side with length 2. A circle is drawn touching one small side and two large sides is drawn. Diagonal of the rectangle is making angle of major 30°. Find length of chord made by diagonal of rectangle as shown in figure.
Step 1: (Constructions)
Draw perpendicular to chord to side of rectangle (It will also pass through center of that circle).
Draw perpendicular to the large side of rectangle passing through center of circle
Join center of circle and starting or ending point of chord
Step 2:
Radius = 1
AB = 2√3 ------(Triangle with 30-60-90 angles and side = 2)
AD = 1 ------(Radius = 1)
⇒ BD = 2√3 - 1 ------(AB - AD)
In Triangle OCD, angle at O is 30°
OD = 1 -----(Radius = 1)
CD = 1/√3 -----(Trigonometry)
Let OM = x
Step 3:
In triangle CMB
Observe 30-60-90 triangle
CM = 2/√3 + x
CB = 1/√3 + 2√3 - 1 = 7/√3 - 1
\[sin(30) = \frac{CM}{CB}\]
\[\frac{1}{2} = \frac{\frac{2}{\sqrt{3}}+x}{\frac{7}{\sqrt{3}}-1}\]
\[ \Rightarrow\frac{7}{\sqrt{3}}-1= \frac{4}{\sqrt{3}}+2x\]
\[ \Rightarrow x=\frac{\sqrt{3}-1}{2}\]
Step 4:
In triangle OMN
M making 90°
\[ \Rightarrow OM^2 + MN^2 = ON^2\]
\[ \Rightarrow \left(\frac{\sqrt{3}-1}{2}\right)^2 + a^2 = 1^2\]
\[ \Rightarrow \left(\frac{4-2\sqrt{3}}{4}\right) + a^2 = 1\]
\[ \Rightarrow a^2 = 1-\left(\frac{4-2\sqrt{3}}{4}\right)\]
\[ \Rightarrow a^2 =\frac{2\sqrt{3}}{4}\]
\[ \Rightarrow a =\frac{\sqrt{2\sqrt{3}}}{2}\]
\[Chord = 2a =\sqrt{2\sqrt{3}}\]
Image Solution:
Solution From @geometri_hayattir:
Puzzle Related to Geometry, Circle, Rectangle